Bahnbrechende mathematische Formel ebnet den Weg für spannende Fortschritte in der Gesundheits-, Energie- und Lebensmittelindustrie
Diffusionsbewegung durch durchlässiges Material kann erstmals exakt modelliert werden
Es wurde eine bahnbrechende mathematische Gleichung entdeckt, die medizinische Verfahren, die Erdgasförderung und die Herstellung von Kunststoffverpackungen in Zukunft verändern könnte.
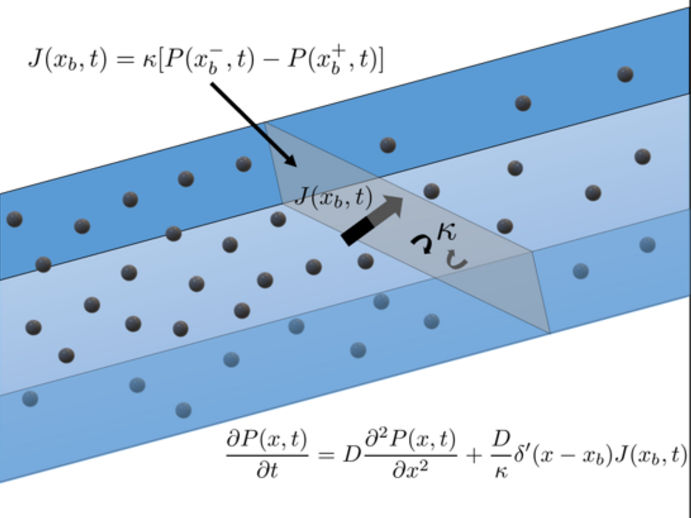
Es wurde eine bahnbrechende neue Gleichung entwickelt, mit der die Diffusionsbewegung durch durchlässiges Material zum ersten Mal exakt modelliert werden kann.
University of Bristol
Die neue Gleichung, die von Wissenschaftlern der Universität Bristol entwickelt wurde, zeigt, dass die Diffusionsbewegung durch durchlässiges Material zum ersten Mal genau modelliert werden kann. Die neue Gleichung wurde ein Jahrhundert nach der ersten Diffusionsgleichung der weltweit führenden Physiker Albert Einstein und Marian von Smoluchowski aufgestellt und stellt einen wichtigen Fortschritt bei der Darstellung von Bewegungen für ein breites Spektrum von Entitäten dar, von mikroskopischen Teilchen über natürliche Organismen bis hin zu vom Menschen hergestellten Geräten.
Bisher waren Wissenschaftler, die sich mit der Bewegung von Teilchen durch poröse Materialien wie biologisches Gewebe, Polymere, verschiedene Gesteine und Schwämme befassten, auf Näherungswerte oder unvollständige Sichtweisen angewiesen.
Die heute in der Fachzeitschrift Physical Review Research veröffentlichten Ergebnisse stellen eine neuartige Technik dar, die in verschiedenen Bereichen wie der Gesundheits-, Energie- und Lebensmittelindustrie interessante Möglichkeiten bietet.
Hauptautor Toby Kay, der in Ingenieurmathematik promoviert, sagte: "Dies ist ein grundlegender Schritt nach vorn seit Einsteins und Smoluchowskis Studien zur Diffusion. Es revolutioniert die Modellierung von diffundierenden Objekten in komplexen Medien aller Größenordnungen, von zellulären Komponenten und geologischen Verbindungen bis hin zu ökologischen Lebensräumen.
"Bisher waren die mathematischen Versuche, die Bewegung durch Umgebungen darzustellen, die mit Objekten übersät sind, die die Bewegung behindern, so genannte durchlässige Barrieren, begrenzt. Mit der Lösung dieses Problems ebnen wir den Weg für spannende Fortschritte in vielen verschiedenen Bereichen, denn durchlässige Barrieren sind für Tiere, Zellorganismen und Menschen alltäglich.
Kreativität in der Mathematik nimmt verschiedene Formen an, und eine davon ist die Verbindung zwischen verschiedenen Ebenen der Beschreibung eines Phänomens. In diesem Fall war es möglich, die neue Gleichung zu finden, indem man die Zufallsbewegung auf mikroskopische Weise darstellte und dann herauszoomte, um den Prozess makroskopisch zu beschreiben.
Weitere Forschung ist erforderlich, um dieses mathematische Werkzeug auf experimentelle Anwendungen anzuwenden, die Produkte und Dienstleistungen verbessern könnten. Die Möglichkeit, die Diffusion von Wassermolekülen durch biologisches Gewebe genau zu modellieren, wird zum Beispiel die Interpretation von diffusionsgewichteten MRT-Messungen (Magnetresonanztomographie) verbessern. Sie könnte auch eine genauere Darstellung der Luftausbreitung durch Lebensmittelverpackungsmaterialien ermöglichen und so bei der Bestimmung der Haltbarkeit und des Kontaminationsrisikos helfen. Darüber hinaus könnte die Quantifizierung des Verhaltens von Tieren bei der Nahrungssuche, die mit makroskopischen Hindernissen wie Zäunen und Straßen interagieren, bessere Vorhersagen über die Folgen des Klimawandels für den Naturschutz ermöglichen.
Der Einsatz von Geolokatoren, Mobiltelefonen und anderen Sensoren hat in den letzten 20 Jahren dazu geführt, dass die Bewegungsdaten in immer größerer Menge und Qualität erfasst werden. Dies hat den Bedarf an ausgefeilteren Modellierungswerkzeugen zur Darstellung der Bewegung verschiedenster Lebewesen in ihrer Umwelt, von natürlichen Organismen bis hin zu vom Menschen geschaffenen Geräten, deutlich gemacht.
Der Hauptautor Dr. Luca Giuggioli, außerordentlicher Professor für Komplexitätswissenschaften an der Universität Bristol, sagte: "Diese neue fundamentale Gleichung ist ein weiteres Beispiel dafür, wie wichtig es ist, Werkzeuge und Techniken zu entwickeln, um die Diffusion in heterogenen Räumen darzustellen, d. h. wenn sich die zugrunde liegende Umgebung von Ort zu Ort ändert.
"Sie baut auf einer weiteren lang erwarteten Lösung eines mathematischen Rätsels zur Beschreibung zufälliger Bewegung in einem begrenzten Raum im Jahr 2020 auf. Diese jüngste Entdeckung ist ein weiterer bedeutender Schritt nach vorn bei der Verbesserung unseres Verständnisses von Bewegung in all ihren Formen und Ausprägungen - zusammenfassend als Mathematik der Bewegung bezeichnet -, die viele spannende potenzielle Anwendungen hat."
Hinweis: Dieser Artikel wurde mit einem Computersystem ohne menschlichen Eingriff übersetzt. LUMITOS bietet diese automatischen Übersetzungen an, um eine größere Bandbreite an aktuellen Nachrichten zu präsentieren. Da dieser Artikel mit automatischer Übersetzung übersetzt wurde, ist es möglich, dass er Fehler im Vokabular, in der Syntax oder in der Grammatik enthält. Den ursprünglichen Artikel in Englisch finden Sie hier.
Weitere News aus dem Ressort Wirtschaft & Finanzen
Diese Produkte könnten Sie interessieren
VEGABAR /VEGAPULS / VEGAPOINT von VEGA Grieshaber
Füllstand- und Drucksensoren - bis 150 °C CIP-reinigbar
Erfahren Sie mehr über die hygienischen, zuverlässigen und effizienten Sensoren von VEGA
BUCHI NIR Solutions for the food industry von NIR-Online
Kontrollieren Sie Prozesse in Echtzeit - selbst unter rauen Bedingungen
Feuchte, Protein, Öl, Asche, uvm. gleichzeitig messen
Holen Sie sich die Lebensmittel- und Getränke-Branche in Ihren Posteingang
Ab sofort nichts mehr verpassen: Unser Newsletter für die Lebensmittel- und Getränkeindustrie bringt Sie jeden Dienstag und Donnerstag auf den neuesten Stand. Aktuelle Branchen-News, Produkt-Highlights und Innovationen - kompakt und verständlich in Ihrem Posteingang. Von uns recherchiert, damit Sie es nicht tun müssen.
