Une formule mathématique novatrice ouvre la voie à des avancées passionnantes dans les domaines de la santé, de l'énergie et de l'industrie alimentaire.
Pour la première fois, le mouvement diffus à travers un matériau perméable peut être modélisé de manière exacte.
Une équation mathématique révolutionnaire a été découverte, qui pourrait transformer à l'avenir les procédures médicales, l'extraction du gaz naturel et la production d'emballages en plastique.
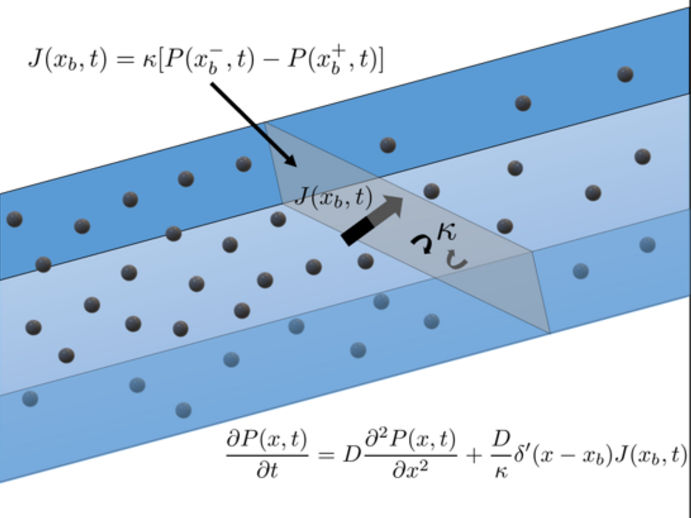
Une nouvelle équation révolutionnaire a été mise au point pour modéliser exactement, pour la toute première fois, le mouvement diffus à travers un matériau perméable.
University of Bristol
La nouvelle équation, élaborée par des scientifiques de l'université de Bristol, indique que le mouvement diffusif à travers un matériau perméable peut être modélisé exactement pour la toute première fois. Elle intervient un siècle après que les physiciens de renommée mondiale Albert Einstein et Marian von Smoluchowski ont dérivé la première équation de diffusion et marque un progrès important dans la représentation du mouvement pour un large éventail d'entités allant des particules microscopiques et des organismes naturels aux dispositifs fabriqués par l'homme.
Jusqu'à présent, les scientifiques qui étudiaient le mouvement des particules à travers des matériaux poreux tels que les tissus biologiques, les polymères, diverses roches et éponges, devaient s'appuyer sur des approximations ou des perspectives incomplètes.
Les résultats, publiés aujourd'hui dans la revue Physical Review Research, constituent une nouvelle technique offrant des possibilités intéressantes dans un large éventail de domaines, notamment la santé, l'énergie et l'industrie alimentaire .
L'auteur principal, Toby Kay, qui achève un doctorat en mathématiques de l'ingénierie, a déclaré : "Cette découverte marque une étape fondamentale depuis que les chercheurs ont commencé à travailler sur les questions de santé : "Cela marque une avancée fondamentale depuis les études d'Einstein et Smoluchowski sur la diffusion. Elle révolutionne la modélisation des entités qui diffusent dans des milieux complexes à toutes les échelles, des composants cellulaires aux composés géologiques en passant par les habitats environnementaux.
"Auparavant, les tentatives mathématiques de représenter le mouvement à travers des environnements parsemés d'objets qui entravent le mouvement, appelés barrières perméables, étaient limitées. En résolvant ce problème, nous ouvrons la voie à des avancées passionnantes dans de nombreux secteurs différents, car les barrières perméables sont couramment rencontrées par les animaux, les organismes cellulaires et les humains."
La créativité en mathématiques prend différentes formes et l'une d'entre elles est la connexion entre différents niveaux de description d'un phénomène. Dans ce cas, en représentant le mouvement aléatoire de manière microscopique, puis en faisant un zoom arrière pour décrire le processus de manière macroscopique, il a été possible de trouver la nouvelle équation.
Des recherches supplémentaires sont nécessaires pour appliquer cet outil mathématique à des applications expérimentales, ce qui pourrait améliorer les produits et les services. Par exemple, le fait de pouvoir modéliser avec précision la diffusion des molécules d'eau dans les tissus biologiques permettra de mieux interpréter les résultats de l'IRM (imagerie par résonance magnétique) pondérée par la diffusion. Elle pourrait également offrir une représentation plus précise de la diffusion de l'air à travers les matériaux d'emballage alimentaire , ce qui aiderait à déterminer la durée de conservation et le risque de contamination. En outre, la quantification du comportement des animaux en quête de nourriture qui interagissent avec des barrières macroscopiques, telles que des clôtures et des routes, pourrait permettre de mieux prédire les conséquences du changement climatique à des fins de conservation.
Grâce à l'utilisation de géolocalisateurs, de téléphones mobiles et d'autres capteurs, la révolution du pistage a permis de générer des données sur les mouvements dont la quantité et la qualité n'ont cessé de croître au cours des vingt dernières années. Cela a mis en évidence la nécessité de disposer d'outils de modélisation plus sophistiqués pour représenter le mouvement d'entités très diverses dans leur environnement, des organismes naturels aux dispositifs fabriqués par l'homme.
L'auteur principal, le Dr Luca Giuggioli, professeur associé en sciences de la complexité à l'université de Bristol, a déclaré : "Cette nouvelle équation fondamentale est un autre exemple de l'importance de construire des outils et des techniques pour représenter la diffusion lorsque l'espace est hétérogène, c'est-à-dire lorsque l'environnement sous-jacent change d'un endroit à l'autre.
"Elle s'appuie sur une autre résolution attendue depuis longtemps, en 2020, d'une énigme mathématique pour décrire le mouvement aléatoire dans un espace confiné. Cette dernière découverte est une nouvelle étape importante dans l'amélioration de notre compréhension du mouvement sous toutes ses formes - collectivement appelée les mathématiques du mouvement - qui a de nombreuses applications potentielles passionnantes."
Note: Cet article a été traduit à l'aide d'un système informatique sans intervention humaine. LUMITOS propose ces traductions automatiques pour présenter un plus large éventail d'actualités. Comme cet article a été traduit avec traduction automatique, il est possible qu'il contienne des erreurs de vocabulaire, de syntaxe ou de grammaire. L'article original dans Anglais peut être trouvé ici.
Autres actualités du département economie & finances
Recevez les dernières actualités du secteur de l'alimentation et des boissons
Ne manquez plus aucune actualité : notre newsletter consacrée à l'industrie alimentaire et des boissons vous informe tous les mardis et jeudis. Les dernières nouvelles du secteur, les produits phares et les innovations - de manière compacte et compréhensible dans votre boîte de réception. Recherché par nos soins, pour que vous n'ayez pas à le faire.
